Ajedrez electrónico – cómo funciona su inteligencia?

Primero observemos cómo jugamos los humanos. Lo primero que hacemos es mirar el tablero y reconocer las piezas, sus posiciones, a qué piezas amenazan, qué piezas nos amenazan, también hacemos una aritmética de amenazas…

Armamos una estrategia tratando de anticipándonos al adversario, calculando mentalmente las jugadas siguientes a una hipotética jugada que hagamos. Podemos pensar:

-Si muevo este peón, y entonces él, mueve aquí su dama  mi caballo se verá amenazado, o puede que se enroque. También puede hacer todos estos movimientos que a priori yo diría que no son útiles. También puedo mover este caballo, y sus posibles respuestas son x,y,z…

Esto es lo que llamaríamos un análisis en profundidad. La profundidad de este análisis depende de nuestra habilidad para jugar al ajedrez. Lo que estamos haciendo es ver cuáles son nuestras mejores jugadas, e imaginar las posibles mejores respuestas de nuestro oponente. Luego hacemos una valoración, y si creemos que salimos ganando, ejecutamos ese movimiento. Grosso modo.

El problema del horizonte de ajedrez electrónico

Cuando he dicho:

estos movimientos que a priori yo diría que no son útiles

He introducido, sin darme cuenta**, el clásico problema del horizonte. Un ejemplo podría ser el siguiente:

Si nosotros saltamos por la ventana de un rascacielos, sabemos que nos vamos a estrellar contra el suelo. Sin embargo, si en un futuro no muy lejano un ordenador, que también tiene sentimientos, me escuchase a mí cantando Entre dos tierras, también decidiría tirarse por la ventana. Él no sabría lo que hay al final del rascacielos. Sólo sabe que debajo de cada piso, hay otro. Hará un cálculo, comenzando en el piso desde el que salta y hacia abajo, previendo con qué se va a encontrar. Si puede calcular el número de casos suficiente, sabrá que llegará un momento en el que se estampe contra los adoquines.

Pero en la práctica, la capacidad de cálculo de los ordenadores es limitada. Esta limitación es la que genera el problema del horizonte: al no poder calcular la totalidad de casos no sabe qué hay al final. En el tema del ajedrez pasa igual: no puede analizar todos los casos posibles, hay un horizonte que no puede sobrepasar y, por tanto, le falta información. Para que os hagáis una idea, se calcula que el número de posibles combinaciones de piezas después de los diez primeros movimientos es de alrededor de 165.518.829.100.544.000.000.000.000. Un ordenador rapidísimo, capaz de evaluar  un millón de posiciones por segundo, necesitaría más de 7 billones de años (mucho más que la edad del universo estimada hoy en día) para generar todas las combinaciones posibles y decidir cuál es la mejor.

A nosotros los hombres nos pasa igual. A las mujeres no estoy seguro: la novia de un amigo mío parece conocer siempre la última consecuencia de cada decisión que mi colega toma. En cualquier caso, podemos compensar el problema del horizonte con nuestra capacidad de razonamiento. Un ordenador… veremos qué hace un poco más adelante.

**Así soy yo.

La función de evaluación o La magia de la heurística

La heurística (función de evaluación o función heurística) es la parte de la IA que se encarga de darle un valor a una jugada.

¿Cómo lo hace? Pues como nosotros queramos. En realidad como quiera el programador de la IA. En general, supondremos que una jugada es buena (tiene un valor alto) si nos acerca a la victoria, y mala (valor bajo o negativo) si nos hace perder.  Dado un estado de juego (un tablero de juego con las piezas sobre él, cada una en una posición), le daremos un valor basado en esas piezas en concreto en esas posiciones en concreto. Este valor depende de muchos factores:

• 
  
  Si nos encontramos ante un jaquemate (lo que significaría el fin de la partida, un estado terminal) a nuestro favor, obviamente le daremos un valor infinito (positivo, claro), puesto que hemos ganado.
  
  
• 
  
  No obstante, si sucede lo contrario (que perdemos), le daremos un valor infinitamente negativo.
  
  
• 
  
  Los valores intermedios (cuando la partida no está finalizada) dependen de los criterios que use el programador, y esto depende de su conocimiento del ajedrez. Como ejemplo, supongamos que tenemos una ventaja material de 20 puntos (cada pieza en ajedrez tiene un valor, y suele ser algo bastante representativo). Es decir, supongamos que la dama y las dos torres de nuestro oponente se han inmolado. En esta situación podemos darle un buen valor al estado de juego, ya que muy mal tendríamos que jugar para perder esa ventaja.
  
  

Hay muchos más criterios a tener en cuenta, como la posición de las piezas. Una de las implementaciones de los modernos programas de ajedrez es que también tienen partidas guardadas, “aprendidas”, que utilizan para evaluar los estados de juego. Si el estado aparece en varias de esas partidas, y en todas esas partidas acaba ganando nuestro color, podemos inferir que es bueno para nosotros.

Esta acción de atribuir valores a un tablero lo hace la función heurística de la IA, y es, en mi opinión, la parte de la IA que la hace más o menos inteligente.

El cerebro del programa: el algoritmo MiniMax

Este algoritmo es lo que podríamos llamar el grueso del cerebro de la IA. Es el algoritmo que calcula las jugadas y elige la más beneficiosa. Como dije en la introducción, nosotros imaginamos nuestra jugada, las respuestas del adversario, las nuestras, y así sucesivamente. Para tantas jugadas y con tanta profundidad como podamos. De esto es de lo que se encarga este algoritmo. Su funcionamiento es muy sencillo:

En el ajedrez hay dos jugadores. Pues vamos a llamarlos Max, y Min. Y supongamos que Max juega con Blancas y Min con Negras. También  nuestra IA conoce las reglas del juego: cómo se mueven las piezas, el jaque mate, tablas, etc. El algoritmo, en general (ya que hay muchas variaciones y mejoras), es el siguiente:

1. 
   
   A Max le toca mover. Ejecuta un movimiento. Ahora le toca a Min, que ejecuta otro movimiento. Le toca a Max… y así sucesivamente, hasta que el algoritmo alcance el nivel de profundidad que queramos.
   
   
2. 
   
   Ahora, que Max haga un movimiento distinto. Que Min ejecute su respuesta. Ahora Max… y asi, de nuevo, hasta que alcancemos la profundidad deseada.
   
   
3. 
   
   Y esto con todos los posibles movimientos de Max.
   
   

Este es un árbol de juego de profundidad n=2 para el juego del tres en raya. Hay un nodo raíz y 5 nodos hijos.

Lo que generamos es un árbol de jugadas. El nodo raíz es el tablero inicial de Max. Este nodo raíz es también nodo padre y sus nodos hijos son tableros de Min. El árbol se ramifica de forma exponencial, ya que si en cada nodo hay una media de 10 posibles movimientos (o sucesores), el número total de movimientos será 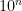donde n será la profundidad de cálculo que queramos alcanzar. Para una profundidad de 4 (esto serían 4 movimientos, dos de Max y dos de Min) tendríamos movimientos que analizar.

Aún nos queda la mejor parte. Este algoritmo que desarrolla el árbol de juego necesita elegir un movimiento. Para ello, aplica la función de evaluación a los nodos terminales. Ahora bien, Max debe escoger, en cada capa o nivel (cada nivel de profundidad), el nodo hijo que tenga un máximo valor (MAXimiza este valor), y Min cogerá el menor de sus nodos hijos (MINimiza este valor). ¿Qué significa esto? Pues que Max escogerá la jugada que le de un mayor beneficio, y Min cogerá la jugada que le de un mayor beneficio a si mismo.

¿Cómo, qué, cuándo? ¿No dijiste que cogía su nodo hijo de mínimo valor? Sí, eso dije. Pero en el caso que nos ocupa, la función de evaluación da puntuaciones buenas a lo que es bueno para Max, y puntuaciones bajas a lo que es malo para Max. Y lo que es malo para Max es bueno para Min, así que Min cogerá lo que peor le venga a Max, es decir: los valores bajos.

Lo que hace este algoritmo es coger la mejor jugada para cada jugador, y la que más beneficio reporte a Max será la jugada que efectúe. Pero veámoslo con más detalle:

Este es un árbol de juego en el que podemos ver los valores que la función heurística atribuye a cada estado de juego.

En el gráfico superior, podemos ver un árbol de juego con nodos terminales. Es algo abstracto, no es un juego en concreto sino una explicación del algoritmo. Olvidaros de todos los valores que veis: en realidad el algoritmo sólo calcula el valor heurístico de los nodos terminales (los 8 nodos de abajo). Los nodos terminales son de Min, la capa superior (los 4 nodos que son sus padres) son nodos Max, los superiores a estos (2) Min y el nodo raíz es un nodo Max. Así pues, cuando el algoritmo tiene los valores heurísticos de los nodos terminales, como es Max quien debe elegir jugada, maximizará su beneficio. Por eso escoge las jugadas de 7 y 15, en la izquierda, y 2 y 8 en la derecha. Me explico: si Max tiene que elegir entre 7 y 1, elige el 7 porque le da más beneficio. Entre 15 y 2, el 15 por lo mismo. Y así con los demás.

Luego le toca a min, que cogerá el valor más pequeño, así que escoge el 7 entre el 7 y el 15, y el 2 entre el 2 y el 8. La elección se hace desde abajo hacia arriba, y la función heurística sólo se aplica en los nodos terminales. Otro gráfico, de la wikipedia, que es bastante explicativo por sí sólo llegados a este punto:

Otro árbol de juego MiniMax

Digo que el algoritmo hace ascender los valores de los estados terminales, pero también debe hacer ascender, de alguna forma, la jugada que lo ha llevado ahí. Si no, el nodo raíz tendría un valor que para nada le serviría, ¡nunca sabría cómo llegó a ese valor!.

Y así es como funciona este algoritmo, de forma resumida. Hay muchísimas optimizaciones y variaciones, que podrían ser objeto de algún otro post, pero por ahora está bien con esto. Para terminar, un algoritmo MiniMax en pseudocódigo:

MiniMax(posicionactual, profundidad, jugador)
Si nodoTerminal(posicionactual,profundidad) entonces
resultado.Valor = funcionHeuristica(posicionactual);
resultado.Camino = nulo;
devuelve resultado;
si no
sucesores = generaSucesores(posicionactual,jugador);
si estaVacio(sucesores) entonces
resultado.Valor = funcionHeuristica(posicionactual);
resultado.Camino = nulo;
devuelve resultado;
si no
resultadoMejor.Valor = menosInfinito;
para cada sucesor de sucesores
resultadoSucesor = MiniMax(sucesor, profundidad-1, contrario(jugador));
si resultadoMejor.Valor < -resultadoSucesor.Valor entonces
resultadoMejor.Valor = resultadoSucesor.Valor;
resultadoMejor.Camino = sucesor;
fin si;
fin para;
devuelve resultadoMejor;
fin si;
fin si;
fin MiniMax;